METU has an annual Spring Festival. During the festival, there are various activities all around the campus. People dance and sing and student communities show off with their activities. Dero and Bico are going to spend some time together in the fest. They wish to see as many student community activities as possible. They visit the gathering place of student communities, Devrim Stadium. There, Dero and Bico can sit anywhere on a straight line, but they want to sit the best possible point they can. The best point for them is the point where they can see the most community activities. (Note that there can be more than one such point.)

For the sake of simplicity:

• All student community activities will be considered as a single point in cartesian coordinate system.
• Dero and Bico can sit at any point on x axis. Moreover, they will always stay together and sit on the exact same spot. We can consider them as a single person and represent them with a point in cartesian coordinate system.
• Dero and Bico have a viewing angle of 90 degrees, and they always look directly towards the north, in the +y direction. In other words, their view is symmetric along the line \(x = p_x\) where \(p_x\) is the \(x\) coordinate of their standing point.

The following graph will help clear things out:

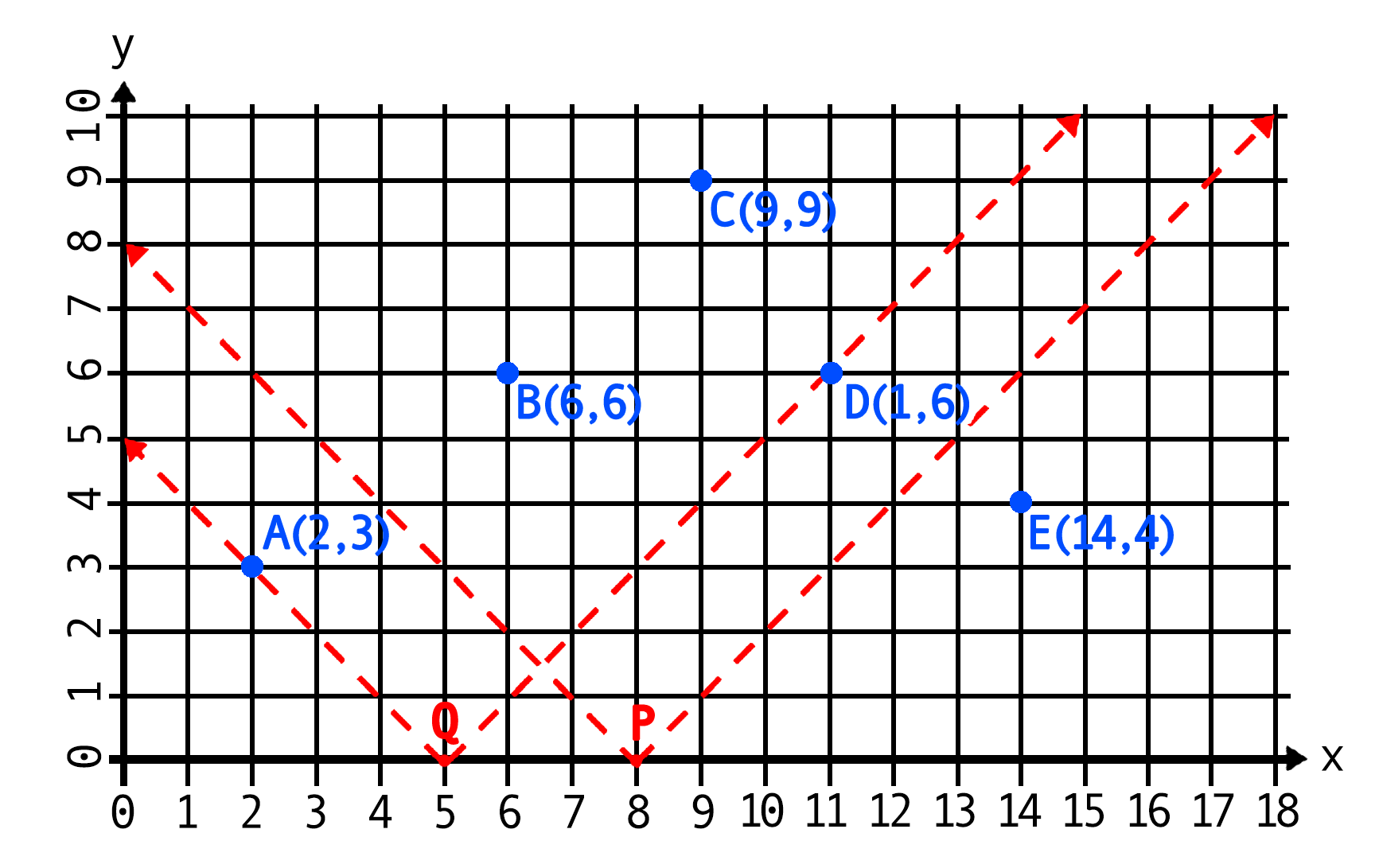
Help Dero and Bico by finding the maximum numbers of student activities they can see from the best point they can sit. You do not need to find the coordinates of the best point(s). Two or more activities on a straight line do not block each other from being seen. In other words, Dero and Bico can see every activity in their sight.

Input

On the first line, there is a positive integer \(N\), denoting the total number of activities present in the scene. Each of the next \(\mathbf{N}\) lines contains two integers separated with a single space, \(\mathbf{x_i}\) and \(\mathbf{y_i}\), denoting the Cartesian coordinate of the i-th community activity.

Output

A single integer, the maximum number of activities that can be seen.

Constraints

• \(N <= 10000\)
• 1 <= \(\mathbf{x_i}\) <= 10000
• 1 <= \(\mathbf{y_i}\) <= 500

Example

Input

4
2 4
2 3
3 5
6 7

Output

4