Being compassionate towards all animals, Deno adopted and took care of Dano, who escaped from the truck that was taking Dano to the slaughterhouse. In a short amount of time Dano grew accustomed to Deno's friendship, is happy and healthy, and now enjoys running around and grazing in the fields, like few from their Kin. Among the volunteers in the sanctuary farm, Dano likes Deno the most and whenever Dano sees Deno, Dano runs towards Deno.

Dano is in a \(\mathbf{N}\times\mathbf{M}\) grass field, and there are \(\mathbf{K}\) trees in that field, each of which located in \((\mathbf{X_i},\mathbf{Y_i})\).

Initially, Dano is located in \((\mathbf{S_x}, \mathbf{S_y})\). To go near Deno's location \((\mathbf{E_x}, \mathbf{E_y})\), Dano starts running. Dano can run in any of the directions \(x\), \(-x\), \(y\), ve \(-y\). Meanwhile, Deno stays perfectly still.

Lastly, for each consecutive second Dano runs in the same direction, they get faster and faster. In other words, if Dano is staying still or is running in other direction and starts running in the \(x\) direction, During the first second they run 1 unit distance, during the second second they run 2 unit disance, in the third second they run 3 unit distance, and for each second Dano runs in that direction, they get faster.

Since Dano gets so happy when they see Deno, Dano does not get hurt if a tree comes in their way and Dano hits that tree. Still, no matter how happy Dano is, they can not pass through a tree.

How long does it take Dano to get near Deno?

*Dano has the option to not cover the maximum distance they can cover. For example, Dano may cover 8 units over 4 seconds by running 1, 2, 3 and 2 units in each respective second.

Input

First line is the dimensions of the grass field, that are \(\mathbf{N}\) and \(\mathbf{M}\).

Second line consists of the initial positions of Dano and Deno, that are \(\mathbf{S_x}\), \(\mathbf{S_y}\), \(\mathbf{E_x}\) and \(\mathbf{E_y}\).

In third line, the number of trees \(\mathbf{K}\) is given.

Finally, Following \(\mathbf{K}\) lines consist of locations \(\mathbf{X_i}\) ve \(\mathbf{Y_i}\) of the trees.

Batch #1:

• \(1 \leq \mathbf{N, M} \leq 40\)
• \(1 \leq \mathbf{K} \leq 500\)

Batch #2:

• \(1 \leq \mathbf{N, M} \leq 400\)
• \(1 \leq \mathbf{K} \leq 10^5\)

Output

Print how long does it take Dano to get near Deno. If Dano cannot reach the point \(\mathbf{E}\) simply print "-1".

Examples

Input:

7 3
1 3 7 3
3
2 3
4 2
6 3

Output:

7

Input:

5 5
1 4 5 4
5
2 2
2 3
2 4
4 4
4 5

Output:

7

Explanation

The grass field in the first example looks like this:

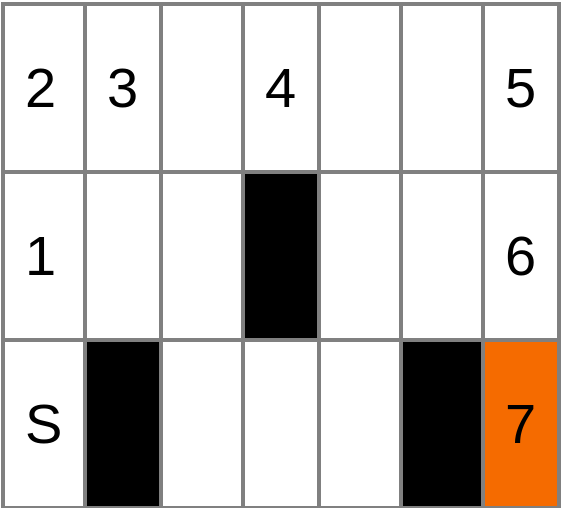
Dano decides to run upwards first. They move 1 unit in the 1st second, then 1 unit in the 2nd second and end up on the top left corner. After that, they turn right and move 1 unit in the 1st second, get faster and move 2 units in the 2nd second. Then they get even faster, move 3 units in the 3rd second and arrive at the top right corner in 5 seconds. After this point, they move downwards and move 2 units in a total of 2 seconds. This way, Dano gets near Deno in 7 seconds in total.