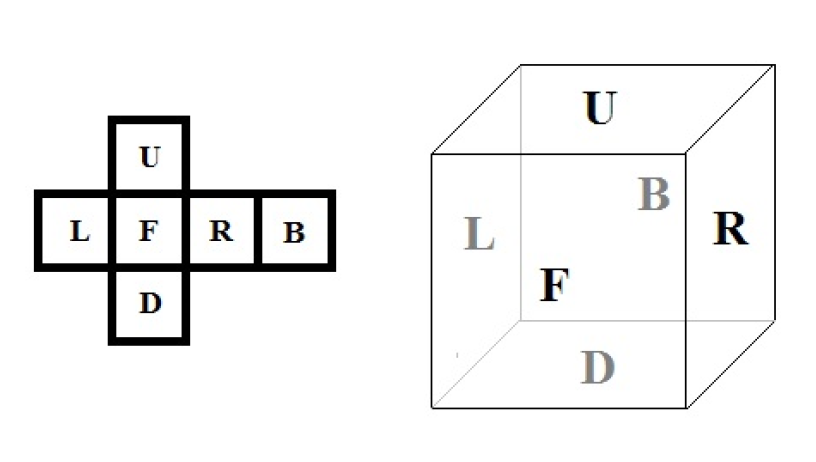
Colored Cubes
View as PDFCan and Birkan have \(N\) colored squares. The i-th square has color \(C_i\). They build a cube using six of the squares. Then they disassemble the cube, build another one and so on. Every time they are trying to build a cube different from the ones they have built before. Two cubes are considered to be same if one of them can be rotated in such way that it looks exactly like the other cube, i.e. the colors on each side are the same. Your task is to count the number of different cubes Can and Birkan can build using their squares.
Input
The first line contains integer \(N\). The following line contains \(N\) integers \(C_i\) separated with single spaces.
Output
The number of different cubes.
Constraints
- 6 ≤ \(N\) ≤ 25
- 1 ≤ \(C_i\) ≤ \(N\)
Samples
Input(stdin)
6
1 1 1 1 2 2
7
1 2 3 4 5 6 7Output(stdout)
2
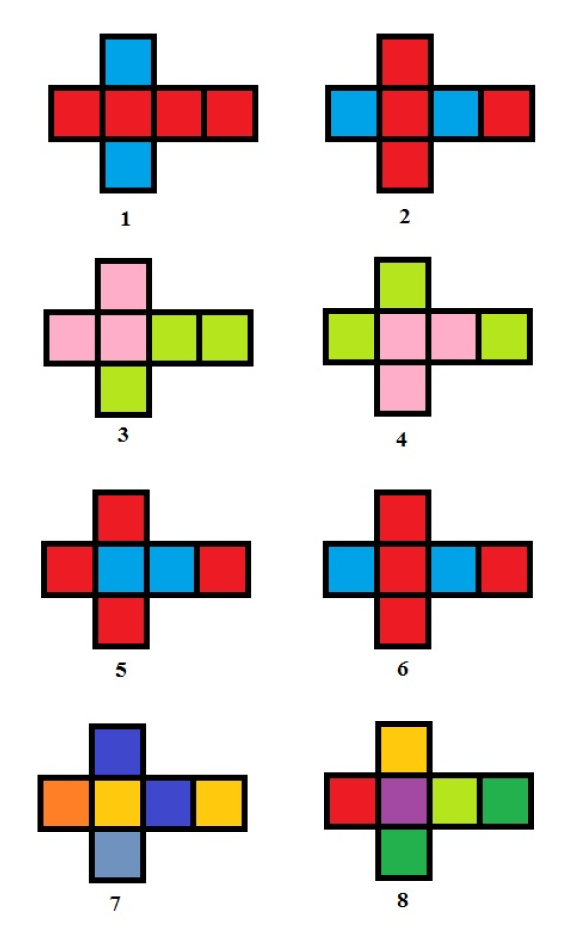
210Notes See a cube structure below. On the figure below:
- cubes 1 and 2 are the same;
- cubes 3 and 4 are the same;
- cubes 5 and 6 are different;
- cubes 7 and 8 are different.