Ozan is a boy who loves computer games. Every day, he goes to the arcade and plays various computer games with his family's permission.

One of the games played by Ozan is a game called "Space Invasion". There are stars and spaceships in this game, and they are all one-dimensional lines. The bard is trying to destroy the spaceship hidden in the sky among the stars. But this spaceship can sometimes hide behind the stars in the game.

Your task in this game is to help Ozan. You need to tell Ozan whether or not Ozan should shoot (whether the spaceship is visible to Ozan) according to the position of the stars and space object given in space.

Input

Each testcase will consist of \(\mathbf{K}\) different tests. In each test, you have to tell whether you can see the spaceship according to Ozan's location.

In the first line of the input, the integer \(\mathbf{K}\) will be given.

For each test:

• In the first line, 7 integers will be given in order. \(\mathbf{M}\) the number of stars in the sky, \(\mathbf{(X_o, Y_o)}\) Ozan's position, \(\mathbf{(X_{u_1}, Y_{u_1})}\) and \(\mathbf{ (X_{u_2}, Y_{u_2})}\) will give the spaceship's position range.
• Next line \(\mathbf{M}\) will give 4 integers, \(\mathbf{(X_{s_1}, Y_{s_1})}\) and \(\mathbf{(X_{s_2}, Y_{s_2})}\) in order , the range of positions where the stars are located.

The constraints:

• \( 0 < \mathbf{K} \leq 1000 \)
• \( 0 \leq \mathbf{M} \leq 1000 \)
• \( 0 \leq X_{s_1}, Y_{s_1}, X_{s_2}, Y_{s_2}, X_{u_1}, Y_{u_1}, X_{u_2}, Y_{u_2}, X_o, Y_o \leq 1000 \)

Output

Output will consist of \(\mathbf{K}\) lines. In each line, you need to say whether Ozan can see the spaceship from the position he is in that test. If Ozan can see the spaceship, you need to print YES, if not, NO. Remember, at least 0.5 unit area of the spaceship must be visible for Ozan to see the spaceship.

Notes

• Ozan always looks in the +y direction with an angle of 180 degrees.
• All the stars will be between Ozan and the spaceship (\( Y_o < Y_{s_1} < Y_{u_1}\) and \( Y_o < Y_{s_1} < Y_{u_2}\)).
• Space objects will always be in Ozan's line of sight. It is also certain that the two points of a spaceship/star cannot collide (distance between two points will be always greater than 0).
• Any two objects in the sky and/or Ozan's positions will not overlap.
• The spaceship will be always parallel to the x-axis.

Example

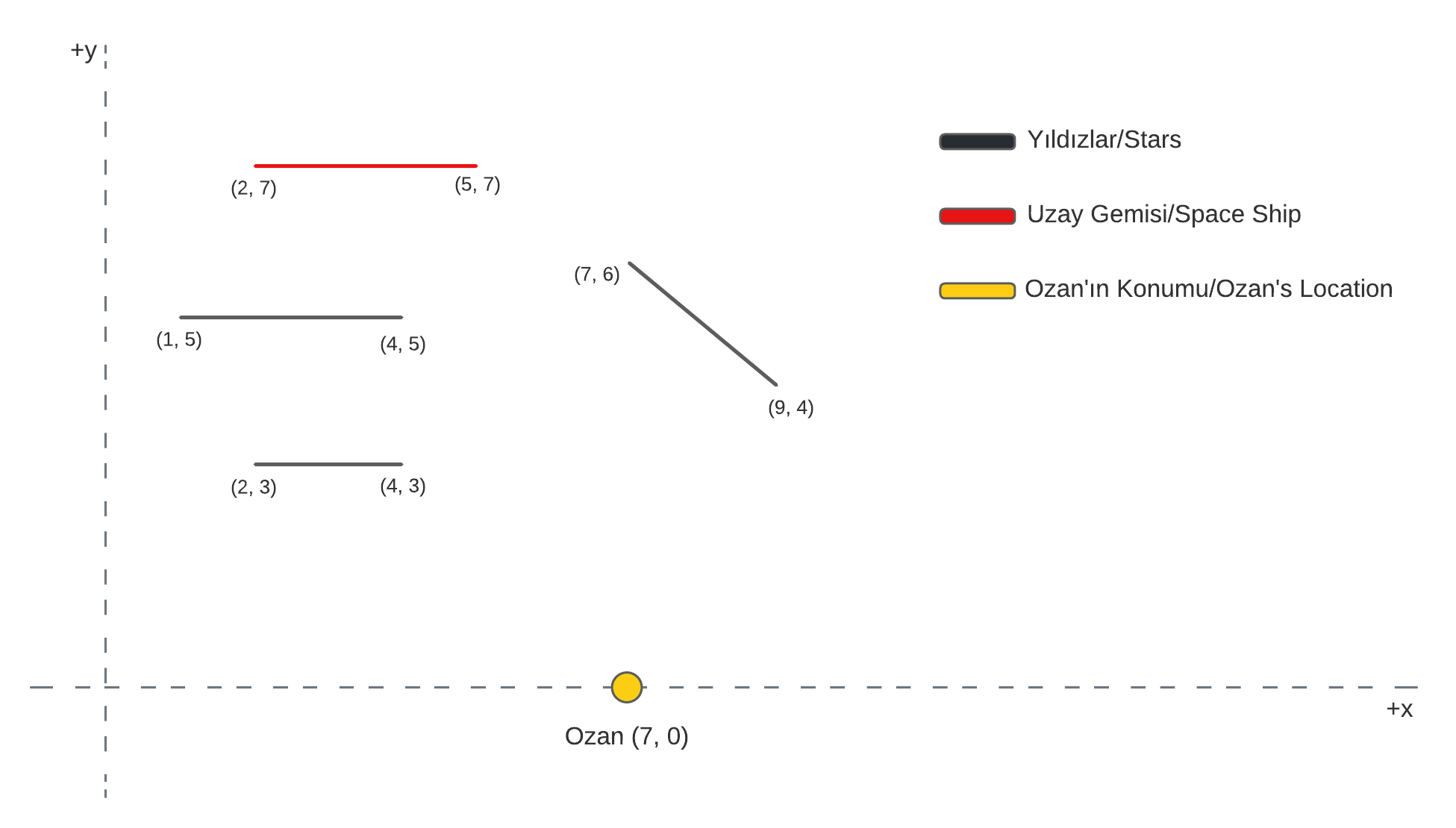
Input:

1
3 7 0 2 7 5 7
1 5 4 5
2 3 4 3
7 6 9 4

Output:

YES

Explanation:

• Although the length of the spaceship is 3 units, 2.2 units can be seen in the testcase.