Two friends, Deni and Ozi are playing a game called Split. In this game, there is an area in which a polygon that has \(\mathbf{N}\) corners. They are splitting the area into 2 areas in this game.

Deni proposes \(\mathbf{M}\) different splits to Ozi. Each split has 2 corners and divides the area into two with the line between those two corners. The area of this line is 0. Ozi takes the area to the right of this line. After considering all of the lines Deni proposes, Ozi needs to choose one of the lines.

Note that any line that can be drawn using 2 points on the polygon doesn't intersect with any other edge of the polygon, so the given polygon is always convex. Also, the polygon doesn't have any self-intersections. Ozi is happy only when he takes the most amount of the area that's available to him. Can you help Ozi to choose the line which makes Ozi happy?

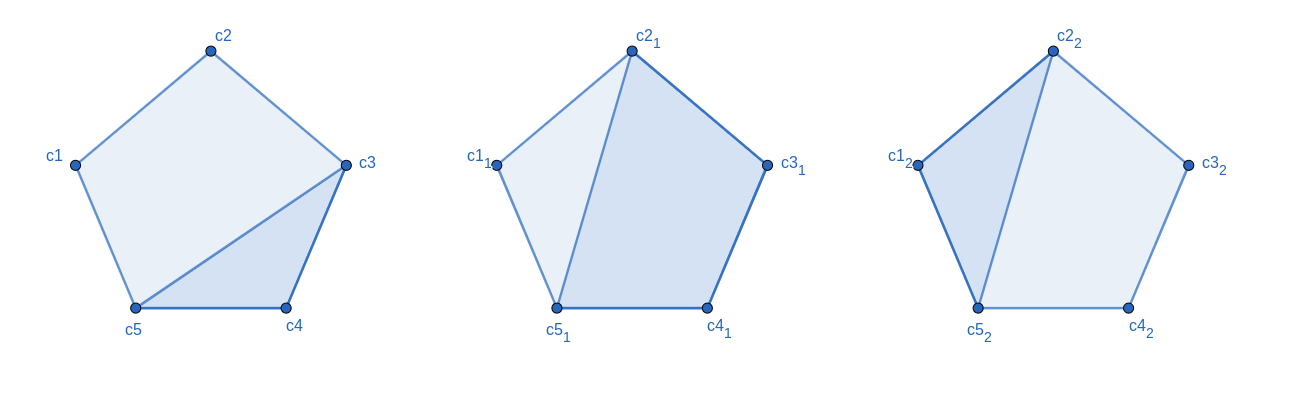
You can see a pentagon on the image above. For this pentagon, Deni proposes 3 splits which are \((5, 3)\), \((5, 2)\) and \((2, 5)\). Note that \((5, 2)\) and \((2, 5)\) result in different amounts of area for Ozi. The areas to the right of the lines are darker, those are the areas that Ozi is able to take. In between those 3 splits Ozi chooses the split which has the biggest are on its right \((5, 2)\).

Input

At the first line, the number of points on polygon \(\mathbf{N}\) and the number of different splits Deni gives to Ozi \(\mathbf{M}\) are given.

In the following, \(\mathbf{N}\) lines, the integers \(\mathbf{X_i}\) and \(\mathbf{Y_i}\), coordinates of the \(i^{th}\) point on the polygon are given.

In the following \(\mathbf{M}\) lines, \(\mathbf{P1_{i}}\) and \(\mathbf{P2_{i}}\), the points that constitute for the \(i^{th}\) split is given.

• \( 4 \leq \mathbf{N} \leq 2\cdot 10^5 \)
• \( 1 \leq \mathbf{M} \leq 2\cdot 10^5 \)
• \( 0 \leq \mathbf{X_i}, \mathbf{Y_i} \leq 10^6 \)
• \( 1 \leq \mathbf{P1_i}, \mathbf{P2_i} \leq \mathbf{N} \)

Output

Only the area which makes Ozi happy should be printed.

Your output will be considered correct if its absolute or relative error is less than 0.0001.

Examples

Input 1:

4 2
5 0
0 0
0 5
5 5
3 1
4 2

Output 1:

12.500000

Input 2:

8 3
1 1
2 0
4 0
5 1
5 3
4 4
2 4
1 3
2 5
3 7
4 7

Output 2:

7.000000

Explanation

Input 1

Both of the splits Deni proposes result in the same area for Ozi. Ozi can choose both of them and has an area of size 12.5.

Input 2

The splits Deni proposes result to areas 4, 7, and 4 for Ozi. Ozi chooses the second one that has an area of size 7.