There are \(\mathbf{N}\) subway stations and \(\mathbf{M}\) distinct lines that connect these stations in Ankara. All of the \(\mathbf{N}\) stations in Ankara have distinct code numbers between \(\mathbf{1}\) and \(\mathbf{N}\). However, all of these stations have been vacant recently.

Due to the global pandemic we are experiencing, citizens of Ankara prefer to stay at home and not to use the subway for transportation. Mayor Mansur, whose agenda includes renewing the subway network, devised starting the restoration in this period to avoid hindering the public transportation when things go back to normal.

Nevertheless, Mansur does not know when things will go back to normal, and when the pandemic ends, citizens of Ankara, who missed their city a lot, will use the subway network to travel around the city extensively. If this happens when an important station is under construction (i.e. not active), public transportation will be hindered greatly. As a solution, Mansur wants to begin the restoration of the subway network with the important stations to keep the negative impact of this process as minimal as possible even if things go back to normal earlier than anticipated.

Mansur's advisors are eager to help him with this challenge. They advise listing the critical stations and restoring those stations first. If a station is critical, then there will be a station not reachable from all stations if this (critical) station is not working. However, Mansur's advisors are quite busy, and they don't have enough time to list the critical subway stations of Ankara.

Can you help Mansur's advisors list the critical subway stations?

• Note that some of the stations might not be connected to each other via a path. So, a station \(\mathbf{S}\) is critical if there exists a pair of stations (A, B) both different from \(\mathbf{S}\) such that they are initially connected via the network but will be disconnected if \(\mathbf{S}\) is closed with all related lines.

Input

The initial line consists of the integers \(\mathbf{N}\) and \(\mathbf{M}\).

Each of the following \(\mathbf{M}\) lines consists of two station code numbers and signifies that there exists a direct and intransitive subway line between these two different stations.

• \(2 \leq \mathbf{N} \leq 10^{5}\)
• \(0 \leq \mathbf{M} \leq 10^{5}\)

Output

Exactly two lines. The count of critical stations should be printed in the first line. In the second line, the code numbers of these stations should be printed, also numbers should be sorted.

If there are no critical stations, then only the number of critical stations (0) should be printed.

Examples

Input:

4 3
1 2
2 3
3 4

Output:

2
2 3

Input:

5 6
1 2
1 3
2 3
3 4
4 5
5 3

Output:

1
3

Explanation

1st Input

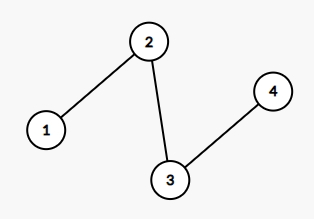
• If station number 2 is removed, there will be no paths between the pairs \((1, 3)\) and \((1, 4)\).
• If station number 3 is removed, there will be no paths between the pairs \((1, 4)\) and \((2, 4)\).

The stations number 2 and 3 are critical.

https://arsiv.cclub.metu.edu.tr/media/mansur01.jpeg

2st Input

• If station number 3 is removed, there will be no paths between the pairs \((1, 4), (1, 5), (2, 4)\) and \((2, 5)\).

Only the station number 3 is critical.

https://arsiv.cclub.metu.edu.tr/media/mansur02.jpeg